Project 4: Night at the Museum
- Assigned: Monday, February 27
- Due: part 1: Friday, March 10, 11:59pm, part 2: Monday April 3rd
- Group policy: Partner-optional
- Collaboration policy: Level 1
In this project you will write code to find the visible area of a guard in a museum. The input will be a simple, non-intersecting polygon in the plane which represents the boundary of the museum, and a point inside this polygon which represents a guard. The goal is to come up with and implement an algorithm that computes and displays the part of the museum that’s visible to the guard. Note that the area that’s visible must be inside the museum (cannot see through the walls), and must be a polygon (cannot have holes and islands). We’ll refer to it as the visible polygon.

To manage complexity we’ll split this project into two parts:
Part 1: Read the polygon and the guard from the user, compute the visible polygon and display it.
Part 2: Extend so that the guard is moving inside the polygon and the visible area is re-computed and displayed as the guard is moving. Move the guard so that the guard does not get stuck in a corner of the polygon.
The interface
Unlike previous projects this one does not need to take any arguments on the command line. To initialize a polygon and the position of a guard inside the polygon you will use the mouse (see examples in class).
The user should press s to start the polygon, then click in the window on the desired location of the vertices, then press e when the polygon is done. The user is expected to enter the polygon in counter-clockwise boundary order. It’s always helpful (and good style) to print a message as the program starts letting the user know the interface:
press 's' to start entering the vertices of the polygon and 'e' to end.
(Please enter the vertices counter-clockwise)
Once the user is done entering the polygon, your code should check whether the polygon is simple (by implementing a function to do that); if it is simple, it should print a message that the test is passed:
testing if polygon is simple: yes
Otherwise, it should print a message that the polygon is not simple and clear the polygon so that the use can start again. This suggest writing aa function to test whether two segments intersect, which might look like this:
\\return true if ab intersects with cd
bool seg_seg_intersect(point 2d a, b, c, d)
Once the user is done entering a simple polygon, the next step is to click on the desired location of the guard. In terms of interface, no specific requirements. You could assume that once the polygon is finished, any mouse click represents a guard; or you can require that the user presses g before clicking on the location of a guard, otherwise the mouse clicks are ignored. This is up to you, but make sure to document it in the Readme file and also while the program is running so that aanyone is able to run your code (for e.g. you could make your keypress function print the interface of your code when key h is pressed).
The guard has to be inside the polygon. You can assume that the user enters a guard that is inside. Ideally (extra credit) you will write a function to test whether a point is inside a polygon —- this is a nice basic algorithm to know about and we’ll talk about this in class. If you want to work on this I would suggest you leave it to the end. We’ll discuss the basic idea in class, but the degenerate cases are messy; there is full pseudocode in the O’Rourke textbook which I suggest you check out and follow.
Once the polygon and the guard are set, (call your function to) compute the visible polygon and (call the function to) render it.
Computing the visible polygon
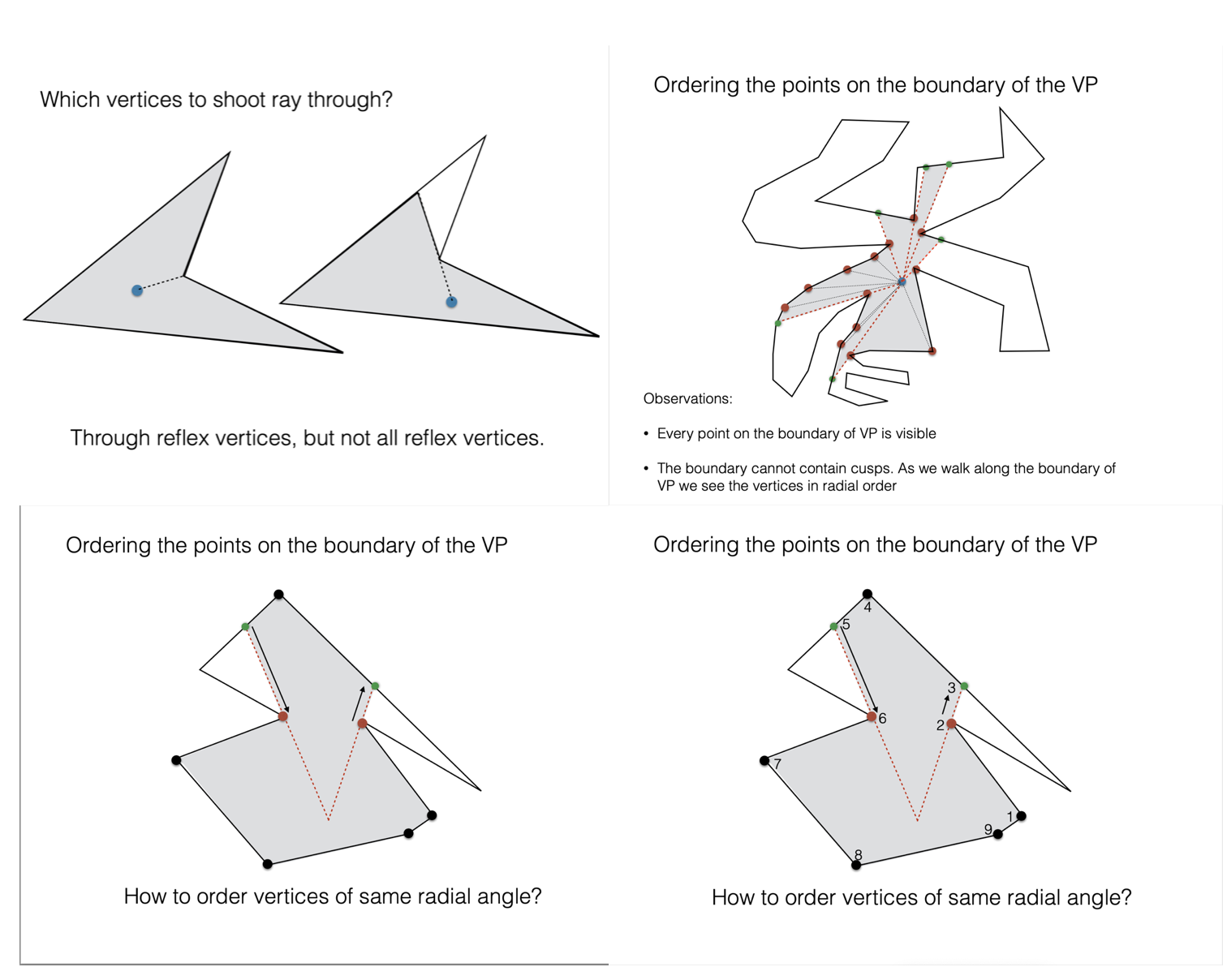
The crux of this project is to come up with an algorithm to compute the visible polygon of the guard. We have not talked specifically about this problem in class and the goal is to come up with a solution on your own. In terms of running time, a quadratic algorithm will suffice.
Towards an algorithm: Draw a couple of polygons and try out some cases. Start with simple polygons, such as convex. How do you compute the visible polygon of a point inside a convex polygon? Now move to non-convex polygons: what is different?
As we try out various cases we make a couple of observations:
- Not all vertices of a non-convex polygon are necessarily visible. This suggests a helper function to determine if a vertex of a polygon is visible from the guard point
p, which might look something like this:
\\return true if polygon[i] is visible from point p
bool isVisible(Vector<point2d> polygon, int i, point2d p)
- The visible polygon consists of the vertices of the museum polygon that are visible, possibly interleaved with points interior to the edges of the museum that represent intersections with rays from the guard. The question is: how to compute these interior points? You will need to shoot rays through some vertices of the museum (which ones?), and, for each ray, find its first intersection with the boundary of the museum. Some questions you will need to answer are: through what vertices do you shoot the rays, and how do you get the points along the boundary of the visible polygon, in the right order?
Rendering the visible polygon
You will need to render the visible polygon filled. Note that visible polygon is not necessarily convex.
You can tell OpenGL to render polygons boundary (GL_LINE mode) or filled (GL_FILL mode) with the following commands:
glPolygonMode(GL_FRONT_AND_BACK, GL_LINE);
//glPolygonMode(GL_FRONT_AND_BACK, GL_FILL);
Something to be aware of is that openGL can only render filled polygons that are convex. This seems like a big limitation, however if you think about it a little it becomes clear that it is not straightforward how to render a non-convex polygon filled: to do that essentially you need to compute the triangulation of the polygon, and then render one triangle at a time. Computing a triangulation of a non-convex polygon is a bigger problem which we’ll talk about in the coming weeks, and OpenGL does not do it as part of the glDraw function.
Even though it’s not convex, the visible polygon has some nice properties that will make rendering it a lot easier!
Rendering a transparent polygon: If you want to do alpha blending with OpenGL, you basically need to specify the color using 4 values, the usual RGB values plus a value that represents the transparency. First, enable blending via glEnable(GL_BLEND) (ideally you would remember to disable it after again when not doing blending, since that will affect performance). While drawing it, specify your method of blending as such: glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA). Make sure to give an alpha value to the colors you’re specifying! 0 is transparent, and 1 is opaque.
You could set up blending in your display() function:
glEnable(GL_BLEND);
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
Then when you want to do blending , specify your color with 4 values, like so:
//set color
GLfloat color[4] = {1, 0, 0, 0.5}; //half-transparent red
glColor4fv(color);
Some ideas to take this a step up
If you want a challenge, try to come up with an improved algorithm that runs in O(n lg n) using a radial sweep (hint: process the vertices in radial order around the guard). Several algorithm are known for computing the visible polygon faster than the quadratic algorithm: the algorithm by Joe and Simpson runs in O(n) time, and the one by Asano in O(n lg n) time. A recent algorithm by Mungiu et al seems to be the fastest in practice. If you are considering an improved algorithm the papers listed below may be helpful. If you want to go down this path you will demo your code in class, get a round of applause, extra credit, and generally feel amazing.
If you try www searching, you may be surprised to find that this is a popular problem with cool applications and visualizations. Here’s some links which I found interesting/relevant:
Some more ideas for extra features:
Implement testing whether the point is inside the polygon (the ray crossing algorithm).
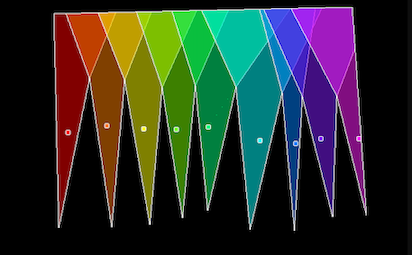
Add more than one moving guards, and render their visible areas transparently, so that the overlap is easy to see, like so: demo1 ; demo2
What and how to turn in
You will receive the assignment on GitHub, but there will be no startup code. To submit, simple push your code into your github repository for this assignment. Do not turn in any object or executable files.
Add a README file containing: a brief, description of the project; info on the interface, i.e. everything one needs to know in order to run your code; a list of known bugs (if any) and when they happen; a list of the main functions you implemented (); any extra features you implemented.
Also: Capture a movie of the screen while you demo your code and upload it to github as demo.mov. To demo, no voice, just run your code and show what it can do (To capture a movie on a Mac press shift+command+5 and then choose the option that says record selected portion).
Evaluation
Your code will be evaluated on the supporting functionality you implemented, on the correctness of the visibility polygon and the number of test cases your algorithm passes, and on the structure and quality of your code.
- appropriate documentation in README.md
- checking if the polygon entered by the user is simple
- checking if the guard entered by the user is inside or outside the polygon [extra credit]
- rendering the visibility polygon filled
- the guard is moving properly and does not get stuck in corners
- multiple (moving) guards [extra credit]
- improved algorithm [extra credit]
Start early, program well and enjoy the proces!
This project is significantly harder than the previous ones and has many pieces that you’ll have to put together (such as segment intersection) while handling degenerate cases. It is crucial that you develop your code one piece at a time, and test before you move on to the next. From the beginning, design your code knowing that you will spend 90% of the time debugging it. Make the debugging easier.